LANDASAN MATEMATIS
Bab ini berisi konsep matematis yang melandasi teori pengolahan citra. Dua operasi matematis penting yang perlu dipahami dalam mempelajari pengolahan citra digital adalah operasi konvolusi dan Transformasi Fourier Konvolusi terdapat pada operasi pengolahan citra yang mengalikan sebuah citra dengan sebuah mask atau kernel, sedangkan Transformasi Fourier dilakukan bila citra dimanipulasi dalam ranah (domain) frekuensi.
3.1 Teori Konvolusi
Operasi yang mendasar dalam pengolahan citra adalah operasi konvolusi. Konvolusi 2 buah fungsi f(x) dan g(x) didefinisikan sebagai berikut :

yang dalam hal ini, tanda, * menyatakan operator konvolusi, dan peubah (variable) a adalah peubah bantu (dummy variable).
Pada operasi konvolusi di atas, g(x) disebut kernel konvolusi atau kernel penapis (filter). Kernel g(x) merupakan suatu jendela yang dioperasikan secara bergeser pada sinyal masukan f(x), yang dalam hal ini, jumlah perkalian kcdua fungsi pada setiap titik merupakan hasil konvolusi yang dinyatakan dengan keluaran h(x).
3.2 Konvolusi Pada Fungsi Dwimatra
Untuk fungsi dengan dua peubah (fungsi dua dimensi atau dwimatra), operasi konvolusi didefinisikan sebagai berikut :
Untuk fungsi malar (kontinyu)
untuk fungsi diskrit
Fungsi penapis g(xy) disebut juga convolution filter, convolution mask, convolution kernel, atau template. Dalam ranah diskrit kernel konvolusi dinyatakan dalam bentuk matriks (umumnya 3 x 3, namun ada juga yang berukuran 2 x 2 atau 2 x 1 atau 1 x 2). Ukuran matriks ini biasanya lebih kecil dari ukuran citra. Setiap elemen matriks disebut koefisien konvolusi.
Ilustrasi konvolusi ditunjukkan pada Gambar 3.1
Ilustrasi konvolusi ditunjukkan pada Gambar 3.1
Gambar 3.1 ilustrasi konvolusi
Operasi konvolusi dilakukan dengan menggeser kernel konvulasi pixel per pixel. Hasil konvolusi disimpan di dalam matriks yang baru.
Contoh 3.1. misalkan citra f(x,y) yang berukuran 5 x 5 dan sebuah kernel atau mask
keterangan Tanda • menyatakan posisi (0,0) dari kernel)
Operasi konvulasi antara citra f(x,y) dengan kernel g(x,y), f(x,y) * g(x,y)
dapat diilustrasikan sebagai berikut :
1. Tempatkan kernel pada sudut kiri atas, kemudian hitung nilai pixel pada posisi (0,0) dari kernel :
Gambar 3.2 Ilustrasi Konvolusi (lanjutan)
Nilai ini dihitung dengan cara berikut :
(0 x 4) + (-1 x 4) + (0 x 3) + (-1 x 6) + (4 x 6) + (-1 x 5) + (0 x 5) + (-1 x 6) + (0 x 6) = 3
2. Geser kernel satu pixel ke kanan, kemudian hitung nilai pixel pada posisi (0,0) dari kernel. Hasil konvulasi = 0. nilai ini dihitung dengan cara berikut :
(0 x 4) + (-1 x 3) + (0 x 5) + (-1 x 6) + (4 x 5) + (-1 x 5) + (0 x 6) + (-1 x 6) + (0 x 6) = 0
3. Geser kernel satu pixel ke kanan, kemudian hitung nilai pixel pada posisi (0,0) dari kernel. Hasil konvulasi = 2. nilai ini dihitung dengan cara berikut :
(0 x 3) + (-1 x 5) + (0 x 4) + (-1 x 5) + (4 x 5) + (-1 x 2) + (0 x 6) + (-1 x 6) + (0 x 2) = 2
Selanjutnya geser kernel satu pixel ke bawah, lalu mulai lagi melakukan konvolusi dari
sisi kiri citra. Setiap kali konvolusi, geser kernel satu pixel ke kanan.
Dengan cara yang sama seperti tadi, maka pixel-pixel pada baris ketiga dikonvolusi
sehingga menghasilkan :
Gambar 3.3 Hasil Konvolusi
Masalah timbul bila pixel yang dikonvolusi adalah pixel pinggir (borders, karena beberapa koefisien konvolusi tidak dapat diposisikan pada pixel-pixel citra (efek "menggantung").
Konvolusi berguna pada proses pengolahan citra seperti:
1. perbaikan kualitas citra (image enhancement)
2. penghilangan derau
3. mengurangi erotan
4. penghalusan/pelembutan citra
5. deteksi tepi, penajaman tepi
6. dll
Karena konvolusi dilakukan per pixel dan untuk setiap pixel dilakukan operasi perkalian dan penjumlahan, maka jelas konvolusi mengkonsumsi banyak waktu. Jika citra berukuran N x N dan kernel berukuran m x m, maka jumlah perkalian adalah dalam orde N2m2. Sebagai contoh jika citra berukuran 512 x 512 dan kernel berukuran 16 x 16, maka ada sekitar 32 juta perkalian yang dibutuhkan. Ini jelas tidak cocok untuk proses yang real time tanpa perangkat keras yang dedicated.
Satu cara mengurangi waktu komputasi adalah mentransformasi citra dan kernel ke dalam ranah frekuensi (dengan menggunakan Transformasi Fourier).K euntungan utama dari penggunaan ranah frekuensi adalah proses konvolusi dapat diterapkan dalam bentuk perkalian langsung.
Proses perubahan fungsi dan ranah ranah spesial ke ranah frekuensi dilakukan melalui Transformasi Fourier. Sedangkan perubahan fungsi dari ranah frekuensi ke ranah spasial dilakukan melalui Transformasi Fourier Balikan (invers).
3.2 Transformasi Fourier
Transformasi Fourier merupakan transformasi paling penting di dalam bidang pengolahan sinyal (signal processing), khususnya pads bidang pengolahan citra.
Umumnya sinyal dinyatakan sebagai bentuk plot amplitudo versus waktu (pada fungsi satu matra) atau plot amplitudo versus posisi spasial (pads fungsi dwimatra). Pada beberapa aplikasi pengolahan sinyal, terdapat kesukaran melakukan operasi karena fungsi dalam ranah waktu/spasial, misalnya pada operasi konvolusi di atas. Operasi konvolusi dapat diterapkan sebagai bentuk perkalian langsung bila fungsi berada dalam ranah frekunsi.
Transformasi Fourier adalah kakas (tool) untuk mengubah fungsi dari ranahwaktu/spasial ke ranah frekuensi. Untuk perubahan sebaliknya digunakanTransformasi Fourier Balikan. Intisari dari Transformasi Fourier adalah menguraikansinyal atau gelombang menjadi sejumlah sinusoida dari berbagai frekuensi, yangjumlahnya ekivalen dengan gelombang awal.
Di dalam pengolahan citra, transformasi Fourier digunakan, untuk menganalisisfrekuensi pada operasi seperti perekaman citra, perbaikan kualitas citra, restorasicitra, pengkodean, dan lain-lain. Dari analisis frekuensi, kita dapat melakukanperubahan frekuensi pada gambar. Perubahan frekuensi berhubungan denganspektrum antara gambar yang kabus kontrasnya sampai gambar yang kaya akan
rincian visualnya. Sebagai contoh, pada proses perekaman citra mungkin terjadipengaburan kontras gambar. Pada gambar yang mengalami kekaburan kontrasterjadi perubahan intensitas secara perlahan yang berarti kebilangan informasifrekuensi tinggi. Untuk meningkatkan kualitas gambar, kita menggunakan penapisfrekuensi tinggi sehingga pixel yang berkontras kabur dapat dinaikkan intensitasnya.
Transformasi Fourier adalah kakas (tool) untuk mengubah fungsi dari ranahwaktu/spasial ke ranah frekuensi. Untuk perubahan sebaliknya digunakanTransformasi Fourier Balikan. Intisari dari Transformasi Fourier adalah menguraikansinyal atau gelombang menjadi sejumlah sinusoida dari berbagai frekuensi, yangjumlahnya ekivalen dengan gelombang awal.
Di dalam pengolahan citra, transformasi Fourier digunakan, untuk menganalisisfrekuensi pada operasi seperti perekaman citra, perbaikan kualitas citra, restorasicitra, pengkodean, dan lain-lain. Dari analisis frekuensi, kita dapat melakukanperubahan frekuensi pada gambar. Perubahan frekuensi berhubungan denganspektrum antara gambar yang kabus kontrasnya sampai gambar yang kaya akan
rincian visualnya. Sebagai contoh, pada proses perekaman citra mungkin terjadipengaburan kontras gambar. Pada gambar yang mengalami kekaburan kontrasterjadi perubahan intensitas secara perlahan yang berarti kebilangan informasifrekuensi tinggi. Untuk meningkatkan kualitas gambar, kita menggunakan penapisfrekuensi tinggi sehingga pixel yang berkontras kabur dapat dinaikkan intensitasnya.
3.2.1 Transformasi Fourier Kontinyu
Yang dalam hal ini,
Baik transformasi Fourier maupun Transformasi Fourier Balikan keduanya dinamakan pasangan transformasi Fourier.
Untuk f(x) real, F(u) adalah fungsi komplek dan dapat dituliskan sebagai :
Untuk f(x) real, F(u) adalah fungsi komplek dan dapat dituliskan sebagai :
Amplitudo atau F(u) spectrum fourier dari f(x) dan didefinisikan sebagai :
Sudut fase spectrum,
Menyatakan pergeseran fase atau sudut fase dari setiap frekuensi u. Dengan mengingat kesamaan Euler,
maka pasangan transformasi euler dapat juga ditulis sebagai
Transformasi fourier untuk fungsi dengan dua peubah adalah
Sedangkan transformasi fourier balikannya adalah
Yang dalam hal ini, x dan y adalah peubah spesial, sedangkan u dan v adalah peubah frekuensi.
Spektrum fourier dari fungsi dua peubah :
Spektrum fourier dari fungsi dua peubah :
Sedangkan sudut fasenya :
Sifat-sifat transformasi Fourier
Jika f(t) ? F(u) dan g(t) ? G(u), maka sifat-sifat transformasi Fourier dirumuskan didalam tabel 3.1
3.2.2 Transformasi Fourier DiskritPada pengolahan sinyal dengan komputer digital, fungsi dinyatakan oleh himpunan berhingga nilai diskrit. Transformasi Fourier Diskrit (TFD) ditujukan bagi persoalan yang tidak menghasilkan solusi transformasi Fourier dalam bentuk fungsi malar.
Tabel 3.1 Sifat-sifat Transformasi Fourier
Tabel 3.1 Sifat-sifat Transformasi Fourier
Bila f(x) yang menerus dibuat diskrit dengan mengambil N buah terokan (sampling) sejarak ?x, yaitu himpunan nilai {f(xo), f(xo + ?x), f(xo + 2?x), ... , f(xo + (N – 1)?x)}.
Jadi,
fs = f(xo + x?x), x = 0, 1, 2, ..., N – 1
Pasangan transformasi Fourier Diskrit untuk fungsi dengan satu peubah :
Pasangan transformasi Fourier Diskrit untuk fungsi dengan satu peubah :
Interpretasi dari TFD adalah sebagai berikut: TFD mengkonversi data diskrit menjadi sejumlah sinusoida diskrit yang frekuensinya dinomori dengan u= 0,1,2,..., N – 1, dan amplitudonya diberikan oleh F(u).
Faktor 1/N pada persamaan F(u) adalah faltor skala yang dapat disertakan dalam persamaan F(u) atau dalam persamaan f(x), tetapi tidak kedua-duanya.
Faktor 1/N pada persamaan F(u) adalah faltor skala yang dapat disertakan dalam persamaan F(u) atau dalam persamaan f(x), tetapi tidak kedua-duanya.
Contoh:
Diketahui fungsi sinyal f(t) dengan hasil penerokan ke dalam nilai-nilai diskrit sebagai berikut
Diketahui fungsi sinyal f(t) dengan hasil penerokan ke dalam nilai-nilai diskrit sebagai berikut
(N = 4): x0 = 0.5, f0 = 2 x1 = 0.75, f1 = 3 x2 = 1.0, f2 = 4 x3 = 1.25,f3 = 4
Transformasi Fourier Diskrit adalah sebagai berikut:
Spektrum fouriernya:
Citra digital adalah fungsi diskrit ranah spasial, dengan dua peubah, x dan y. pada fungsi diskrit dengan dua peubah dan berukuran N X M, pasangan Transformasi Fourier Diskritnya adalah:
Untuk u, x = 0,1,…., N – 1 dan v,y = 0,1…., M – 1.
Algoritma TFD dan balikan dapat diterapkan untuk fungsi diskrit dwimatra. Mula-mula transformasi dilakukan dalam arah x (dengan nilai y tetap). Kemudian, hasilnya ditransformasikan lagi dalam arah y.
Algoritma TFD tidak bagus untuk N yang besar karena komputasinya memakan waktu yang lama. Kompleksitas waktu algoritmanya adalah O(N2). Algoritma yang dikenal cepat untuk menghitung transformasi Fourier diskrit adalah FFT(Fast Fourier Transform).
Gambar 3.4 Contoh Transformasi Fourier 2 Dimensi
(Sumber: http://www.icaen.uiowa.edu/~dip/LECTURE/LinTransforms.html)
Latihan 31. Jelaskan tentang teori konvolusi !
2. Lakukanlah proses konvolusi untuk citra f(x,y) di bawah ini yang berukuran 5 x 5 dan sebuah kernel mask yang berukuran 3 x 3 yang masing-masing adalah sebagai berikut:
2. Lakukanlah proses konvolusi untuk citra f(x,y) di bawah ini yang berukuran 5 x 5 dan sebuah kernel mask yang berukuran 3 x 3 yang masing-masing adalah sebagai berikut:
3. Jelaskan perbedaan teori konvolusi dengan transformasi Fourier!
Pustaka
[BAL82] Ballard, Dana H., Computer Vision, Prentice-Hall, 1982.
[DAV90] Davies, E. R., Machine Vision: Theory, Algorithms, Practicalities, Academic Press, 1990.
[DUL97] Dulimarta, Hans S., Diktat Kuliah Pengolahan Citra, Jurusan Teknik Informatika ITB, 1997.
[FIS94] Fisher, Yuval, Fractal Image Compression: Theory & Application, Springer-Verlag, 1994.
[GAL90] Galbiati, Louis J., Machine Vision and Digital Image Processing Fundamentals, Prentice Hall, 1990.
Citra dijital direpresentasikan dengan matriks. Operasi pada citra dijital pada dasarnya adalah memanipulasi elemen-elemen matriks. Elemen matriks yang dimanipulasi dapat berupa elemen tunggal (sebuah pixel), sekumpulan elemen yang berdekatan, atau keseluruhan elemen matriks. Di dalam bab ini akan diuraikan operasi-operasi dasar pada pengolahan citra digital.
4.1 Aras Komputasi
Operasi-operasi yang dilakukan pada pengolahan citra dapat dikelompokkan ke dalam empat aras (level) komputasi, yaitu aras titik, aras lokal, aras global, dan aras objek [JAI95]. Kita mulai pembahasan komputasi pada aras titik.
1. Aras TitikOperasi pada aras titik hanya dilakukan pada pixel tunggal di dalam citra. Operasi titik dikenal juga dengan nama operasi pointwise. Operasi ini terdiri dari pengaksesan pixel pada lokasi yang diberikan, memodifikasinya dengan operasi operasi lanjar (linear) atau nirlanjar (nonlinear), dan menempatkan nilai pixel baru pada lokasi yang bersesuaian di dalam citra yang baru. Operasi ini diulangi untuk keseluruhan pixel di dalam citra.
Secara matematis, operasi pada aras titik dinyatakan sebagai (Gambar 4.1):
yang dalam hal ini fA dan fB masing-masing adalah citra masukan dan citra keluaran, Otitik dapat berupa operasi lanjar (linear) atau nirlanjar (nonlinear). Yang dimaksud dengan operasi lanjar adalah operasi yang dapat dinyatakan secara matematis sebagai persamaan lanjar, kebalikannya adalah persamaan nirlanjar.
Gambar 4.1 Operasi aras titik pada citra dijital.
a. Berdasarkan intensitas.Nilai intensitas u suatu pixel diubah dengan transformasi h menjadi nilai intensitas baru v:
Contoh operasi titik berdasarkan intensitas adalah operasi pengambangan (thresholding). Pada operasi pengambangan, nilai intensitas pixel dipetakan ke salah satu dari dua nilai, a1 atau a2, berdasarkan nilai ambang (threshold) T:
Jika a1 = 0 dan a2 = 1, maka operasi pengambangan mentransformasikan citra hitam-putih ke citra biner. Dengan kata lain, nilai intensitas pixel semula dipetakan ke dua nilai saja: hitam dan putih. Nilai ambang yang dipakai dapat berlaku untuk keseluruhan pixel atau untuk wilayah tertentu saja (berdasarkan penyebaran nilai intensitas pada wilayah tersebut).
Operasi pengambangan pada citra Lena dengan fungsi transformasi:
menghasilkan citra biner seperti yang diperlihatkan pada Gambar 4.2(a). Persamaan 4.4 menyatakan bahwa pixel-pixel yang nilai intensitasnya di bawah 128 diubah menjadi hitam (nilai intensitas = 0), sedangkan pixel-pixel yang nilai intensitasnya di atas 128 diubah menjadi putih (nilai intensitas = 1) . Algoritma transformasi citra hitam-putih menjadi citra biner ditunjukkan oleh Algoritma 4.1.
Gambar 4.2. (a) Citra biner Lena, (b) citra negatif Lena
Algoritma 4.1. Mengubah citra A menjadi citra biner.
Operasi negatif
yaitu mendapatkan citra negatif (negative image) meniru film negatif pada fotografi dengan cara mengurangi nilai intensitas pixel dari nilai keabuan maksimum. Misalnya pada citra dengan 256 derajat keabuan (8 bit), citra negatif diperoleh dengan persamaan:
| Sedangkan pada citra dengan 128 derajat keabuan, |
Algoritma 4.2. Membuat citra negatif dari sebuah citra dengan 256 derajat keabuan
Pemotongan (clipping)
Operasi ini dilakukan jika nilai intensitas pixel hasil suatu operasi pengolahan citra terletak di bawah nilai intensitas minimum atau di atas nilai intensitas maksimum:
Pemotongan (clipping) termasuk ke dalam operasi pengambangan juga.
Pencerahan citra (image brightening)
Kecerahan citra dapat diperbaiki dengan menambahkan (atau mengurangkan) sebuah konstanta kepada (atau dari) setiap pixel di dalam citra. Secara matematis operasi ini ditulis sebagai
Jika b positif, kecerahan citra bertambah, sebaliknya jika b negatif kecerahan citra berkurang. Lihat contoh pencerahan citra pada Gambar 4.3 yang diterapkan pada citra Zelda. Semula citra Zelda tampak gelap, tetapi dengan menambahkan setiap nilai pixel dengan b = 10, citra Zelda menjadi lebih terang.
Persamaan 4.8 mengisyaratkan bahwa operasi pencerahan citra dapat menghasilkan nilai di bawah nilai intensitas minimum atau d atas nilai intensitas maksimum. Oleh karena itu, operasi clipping perlu diterapkan. Algoritma pencerahan citra ntuk citra dengan 256 derajat keabuan ditunjukkan oleh Algoritma 4.3.
Algoritma 4.3. Pencerahan citra
Gambar 4.3. Kiri: citra Zelda (agak gelap); kanan: citra Zelda setelah operasi pencerahan
b. Berdasarkan geometri.Posisi pixel diubah ke posisi yang baru, sedangkan intensitasnya tidak berubah. Contoh operasi titik berdasarkan geometri misalnya pemutaran (rotasi), pergeseran (translasi), penskalaan (dilatasi), pembetulan erotan (distorsi) geometri (akan dijelaskan kemudian).
c. Gabungan intensitas dan geometri.Operasi ini tidak hanya mengubah nilai intensitas pixel, tapi juga mengubah posisinya. Misalnya image morphing, yaitu perubahan bentuk objek beserta nilai intensitasnya.
2. Aras LokalOperasi pada aras lokal menghasilkan citra keluaran yang intensitas suatu pixel bergantung pada intensitas pixel-pixel tetangganya (Gambar 4.4).
(keterangan: N = neighborhood, yaitu pixel-pixel yang berada di sekitar (x, y) )
Gambar 4.4. Operasi aras lokal
Gambar 4.5. Hasil pendeteksian semua tepi dari citra Lena
3. Aras GlobalOperasi pada aras global menghasilkan citra keluaran yang intensitas suatu pixel bergantung pada intensitas keseluruhan pixel (Gambar 4.6).
Gambar 4.6. Operasi aras global
4. Aras ObjekOperasi jenis ini hanya dilakukan pada objek tertentu di dalam citra. Tujuan dari operasi pada aras objek adalah untuk mengenali objek tersebut, misalnya dengan menghitung rata-rata intensitas, ukuran, bentuk, dan karakteristik lain dari objek. Operasi aras objek adalah operasi yang sangat sulit, karena sebelumnya kita harus dapat menjawab: apakah objek itu, bagaimana menemukannya?
4.2 Operasi Aritmetika
Karena citra dijital adalah matriks, maka operasi-operasi aritmetika matriks juga berlaku pada citra. Operasi matriks yang dapat dilakukan adalah:
1. Penjumlahan atau pengurangan antara dua buah citra A dan B: C(x, y) = A(x, y) ± B(x, y),
2. Perkalian dua buah citra: C(x, y) = A(x, y) B(x, y),
3. Penjumlahan/pengurangan citra A dengan skalar c: B(x, y) = A(x, y) ± c,
4. Perkalian/pembagian citra A dengan sebuah skalar c: B(x, y) = c × A(x, y)
Ditinjau dari aras komputasi, operasi aritmetika termasuk ke dalam operasi aras
titik. Penjelasan masing-masing operasi aritmetika matriks adalah sebagai berikut.
1. Penjumlahan Dua Buah citraPersamaannya:
C adalah citra baru yang intensitas setiap pixel-nya adalah jumlah dari intensitas tiap pixel pada A dan B. Jika hasil penjumlahan intensitas lebih besar dari 255, maka intensitasnya dibulatkan ke 255. Algoritma penjumlahan dua buah citra ditunjukkan pada Algoritma 4.4.
Algoritma 4.4.Penjumlahan dua buah citra
Hasil operasi mungkin bernilai riil, karena itu semua nilai riil tersebut perlu dibulatkan ke nilai bulat terdekat, nilai maksimum adalah 255.
2. Pengurangan Dua Buah CitraPersamaannya:
C adalah citra baru yang intensitas setiap pixel-nya adalah selisih antara intensitas pixel pada A dan B. Ada kemungkinan hasil operasi ini menghasilkan nilai negatif, oleh karena itu, operasi pengurangan citra perlu melibatkan operasi clipping. Contoh aplikasi operasi pengurangan citra adalah untuk memperoleh suatu objek dari dua buah citra [HEN95]. Citra pertama misalnya foto sebuah ruangan yang kosong, citra kedua adalah foto ruangan yang sama tetapi ada orang di dalamnya. Hasil pengurangan citra kedua dengan gambar pertama menghasilkan citra yang latar belakangnya hitam, sedangkan latar depannya (objek orang) berwarna putih. Algoritmanya ditunjukkan pada Algoritma 4.5.
Algoritma 4.5. Pengurangan dua buah citra untuk mendapatkan objek di dalamnya.
3. Perkalian CitraPersamaannya:
Perkalian citra sering digunakan untuk mengoreksi kenirlanjaran sensor dengan cara mengalikan matriks citra dengan matrik koreksi. Jadi, dalam hal ini A adalah citra sedangkan B adalah matriks koreksi. Hasil operasi mungkin bernilai riil, karena itu semua nilai dibulatkan ke nilai bulat terdekat, nilai maksimum adalah 255. Algoritma perkalian citra dengan matriks koreksi ditunjukkan pada Algoritma 4.3. Kita mengasumsikan di sini ukuran citra dan matriks koreksi adalah N ´ N.
Contoh 4.1. [GAL90] Mengalikan citra A dengan matriks koreksi:
Algoritma 4.6. Perkalian citra A dengan matriks koreksi B.
4. Penjumlahan/pengurangan citra dengan skalarPersamaannya:
Penjumlahan citra A dengan skalar c adalah menambah setiap pixel di dalam citra dengah sebuah skalar c, dan menghasilkan citra baru B yang intensitasnya lebih terang daripada A. Kenaikan intensitas sama untuk seluruh pixel, yaitu c. Pengurangan citra A dengan skalar c adalah mengurangkan setiap pixel di dalam citra dengah sebuah skalar c, dan menghasilkan citra baru B yang intensitasnya lebih gelap daripada A. Penurunan intensitas sama untuk seluruh pixel, yaitu c.
Contoh operasi penjumlahan/pengurangan citra dengan sebuah skalar adalah operasi pencerahan citra (lihat pembahasan operasi aras titik).
Baik operasi penjumlahan maupun pengurangan citra dengan sebuah skalar melibatkan operasi clipping. Algoritma penjumlahan/pengurangan citra dengan sebuah skalar sama seperti Algoritma 4.3.
5. Perkalian/pembagian Citra dengan SkalarPersamaannya:
Perkalian citra A dengan skalar c menghasilkan citra baru B yang intensitasnya lebih terang daripada A. Kenaikan intensitas setiap pixel sebanding dengan c. Operasi perkalian citra dengan skalar dipakai untuk kalibrasi kecerahan (callibration of brightness).
Pembagian citra A dengan skalar c menghasilkan citra baru B yang intensitasnya lebih gelap daripada A. Penurunan intensitas setiap pixel berbanding terbalik dengan c. Operasi pembagian citra dengan skalar dipakai untuk normalisasi kecerahan (normalization of brightness).
Algoritma perkalian/pembagian citra dengan sebuah skalar serupa dengan Algoritma 4.3, hanya saja operasi + atau – diganti dengan * atau /.
4.3 Operasi Boolean pada Citra
Selain operasi aritmetika, pemrosesan citra dijital juga melibatkan operasi Boolean (and, or, dan not):
| dalam notasi Bahasa C, ketiga operasi di atas ditulis sebagai: |
C[x][y]=A[x][y]|B[x][y]
C[x][y]=!A[x][y]
Operasi Boolean mempunyai terapan yang penting pada pemrosesan morfologi pada citra biner. Pada citra biner, operasi not dapat digunakan untuk menentukan komplemen dari citra (Gambar 4.7). Algoritma membentuk komplemen dari citra biner ditunjukan oleh Algoritma 4.7.
Gambar 4.7. Hasil operasinot pada citra biner Ganesha
Algoritma 4.7. Membuat citra komplemen dari citra biner
Pada operasi geometrik, koordinat pixel berubah akibat transformasi, sedangkan intensitasnya tetap. Ini berbeda dengan dengan operasi aritmetika yang mana koordinat pixel tetap sedangkan intensitasnya berubah.
Operasi geometri yang dilakukan misalnya translasi, rotasi, penskalaan citra, dan pencerminan citra (flipping). Pengubahan geometri dari citra f(x, y) menjadi citra baru f ’(x, y) dapat ditulis sebagai:
yang dalam hal ini, g1(x) dan g2(y) adalah fungsi transformasi geometrik. Dengan kata lain
a. TranslasiRumus translasi citra:
yang dalam hal ini, m adalah besar pergeseran dalam arah x, sedangkan n adalah besar pergeseran dalam arah y. Jika citra semula adalah A dan citra hasil translasi adalah B, maka translasi dapat diimplementasikan dengan menyalin citra dari A ke B:
Algoritma translasi citra ditunjukkan oleh Algoritma 4.8, sedangkan contoh translasi pada citra camera diperagakan pada Gambar 4.8.
Algoritma 4.8. Operasi translasi citra
Gambar 4.8. Translasi pada citra camera: (a) citra semula, (b)citra hasil translasi dengan m = 30 dan
n = 25. (Terima kasih kepada Nanda Firdausi M atas izin menggunakan output programnya).
b. RotasiRumus rotasi citra:
yang dalam hal ini, q = sudut rotasi berlawanan arah jarum jam (lihat Gambar 4.9). Jika citra semula adalah A dan citra hasil rotasi adalah B, maka rotasi citra dari A ke B:
Gambar 4.9. Model rotasi citra
Jika sudut rotasinya 90°, maka implementasinya lebih mudah dilakukan dengan cara menyalin pixel-pixel baris ke pixel-pixel kolom pada arah rotasi (Gambar 4.10). Rotasi 180° diimplementasikan dengan melakukan rotasi 90° dua kali. Algoritma rotasi citra sejauh 90 derajat berlawanan arah jarum jam ditunjukkan pada Algoritma 4.9, sedangkan rotasi citra sejauh 90 derajat searah jarum jam ditunjukkan pada Algoritma 4.10 [HEN95].
Gambar 4.10. Rotasi citra Lena sejauh 90° berlawanan arah jarum jam
Algoritma 4.8. Rotasi citra sejauh 90° berlawanan arah jarum jam.
Algoritma 4.9. Rotasi citra sejauh 90° searah jarum jam.
Rumus penskalaan citra:
yang dalam hal ini, sx dan sy adalah faktor skala masing-masing dalam arah x dan arah y.
Jika citra semula adalah A dan citra hasil penskalaan adalah B, maka penskalaan citra dinyatakan sebagai:
Operasi zoom out dengan faktor 2 (yaitu, sx = sy = 2) diimplementasikan dengan menyalin setiap pixel sebanyak 4 kali (Gambar 4.11a). Jadi, citra 2 ´ 2 pixel akan menjadi 4 ´ 4 pixel. Algoritma zoom out dengan faktor skala = 2 ditunjukkan oleh Algoritma 4.10. Contoh citra yang diperbesar dua kali diperlihatkan pada Gambar 4.12 (citra kota San Fransisco).
Operasi zoom in (pengecilan) dengan faktor skala = ½ dilakukan dengan mengambil rata-rata dari 4 pixel yang bertetangga menjadi 1 pixel (Gambar 4.11b).
Gambar 4.11. (a) Zoom out dengan faktor skala = 2, (b) Zoom in dengan faktor skala = 1/2
Algoritma 4.10. Zoom out dengan faktor skala = 2
Gambar 4.12. (a) Citra kota San Fransisco (ukuran normal), (b) citra kota San Fransisco setelah
diperbesar 2 kali (sx = sy = 2):
Flipping horizontal adalah pencerminan pada sumbu-Y (cartesian) dari citra A menjadi citra B, yang diberikan oleh:
Flipping vertikal adalah pencerminan pada sumbu-X (cartesian) dari citra A menjadi citra B, yang diberikan oleh:
Algoritma flipping vertikal ditunjukkan oleh Algoritma 4.11 [HEN95].
Pencerminan pada titik asal (cartesian) dari citra A menjadi citra B diberikan oleh:
Pencerminan pada garis x = y dari citra A menjadi citra B diberikan oleh:
Algoritma 4.11. Flipping vertikal.
Pustaka
[HEN95] Hendradjaya, Bayu, Catatan Kuliah Pengolahan Citra, 1995.
[HEN03] Hendrawan, Shanty Meliani, Robust and Non Blind Watermarking pada Citra Dijital dengan Teknik Spread Spectrum, Tugas Akhir Departemen Teknik Informatika, 2003.
[JAI89] Jain, Anil K, Fundamentals of Digital Image Processing, Prentice-Hall International, 1989.
[JAI95] Jain, Ramesh, Machine Vision, McGraw-ill, 1995.
[KER88] Kernighan, Brian W., The C Programming Language 2Th, Prentice Hall, 1988











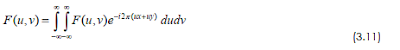









































Komentar
Posting Komentar